Неопределенность в интервале между реперными точками для эталонных термометров сопротивления
Суммарная и расширенная неопределенность градуировки термометра в реперных точках является основой для расчета неопределенности измерения температуры в интервале между точками. Для расчета используется закон распространения неопределенности на интервал, изложенный в Руководстве GUM. Формула имеет следующий вид:

Интерполяционной функцией, в случае применения метода МТШ-90, является W(T), вид функции зависит от диапазона температуры (см. методика построения интерполяционной зависимости МТШ-90). Например, в диапазоне от 0,1 до 660,323 °С функция имеет вид:
W(T) = Wr(T) + a[W(T)-1] + b[W(T)-1]2 + c[W(T)-1]3
Коэффициенты a, b, c зависят от результатов градуировки термометра в реперных точках. Получив аналитические зависимости, связывающие каждый коэффициент с результатами градуировки W(T) в реперных точках, можно рассчитать вариации и ковариации этих коэффициентов, применяя закон распространения неопределенностей. После этого можно рассчитать неопределенность W(T) для любых температур в интервале между реперными точками. Данная задача математически довольно громоздская, хотя может быть решена с применением современных программных средств.

На графике представлена кривая распространения неопределенностей в реперных точках на интервал температур. Из графика видно, что неопределенность при температурах в диапазоне между реперными точками может превышать неопределенности в соседних реперных точках. Это свойство функции МТШ-90, и это говорит о том, что для точных измерений некорректно применять простую линейную интерполяцию между точками для определения неопределенности в интервалах.
На графике, для того, чтобы теоретически оценить влияние корреляции, представлены три кривые для разных вариантов коэффициентов корреляции результатов градуировки в различных точках. Оценка корреляции – сложная задача. Корреляция результатов градуировки в различных точках безусловно существует. Нужно учесть, однако, что основной источник корреляции при калибровке термометра - применение одного и того же измерительного оборудования. Если принять во внимание то, что стандартные неопределенности, связанные с измерением сопротивления, вносят малый вклад в суммарную неопределенность калибровки в реперной точке, и то, что основной вклад в неопределенность в точке вносят сами металлы и настройка процесса затвердевания, то корреляцию можно считать несущественной и ей можно принебречь.
Оценка неопределенности в интервале с помощью функций влияния.
Более удобный метод получения функции распространения неопределенности в интервале между реперными точками – использование альтернативных функций МТШ-90, основанных на функциях влияния. Подробнее об альтернативных зависимостях МТШ-90 можно узнать из публикации ККТ «Guide to the Realization of the ITS-90. Platinum Resistance Thermometry», а также из публикации: White D.R., Saunders P. 2007 The propagation of uncertainty with calibration equations, Meas. Sci.Technol. 18, 2157-2169
Важно подчеркнуть, что предложенные ККТ альтернативные функции не являются аппроксимациями МТШ-90, они не вносят какие-либо погрешности в расчет W(T), а являются просто видоизмененными зависимостями МТШ-90. Для основных диапазонов МТШ-90 функции имеют следующий вид:

Как можно заметить, функции fsn(W), fzn(W), fAl(W) и т.п. принимают значение, равное 1 в точке, соответствующей наименованию функции, и равны 0 в остальных реперных точках. При отсутствии корреляции между точками, эти функции можно применять, для изучения влияния каждой реперной точки отдельно на неопределенность в интервале. 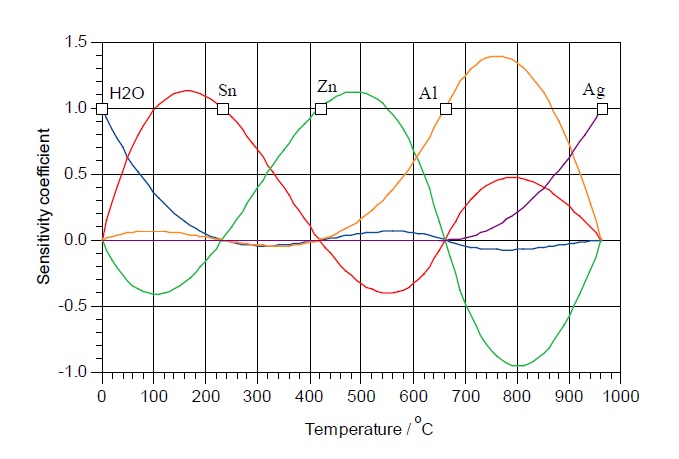
На рисунке изображены функции влияния в диапазоне 0,01 – 660,323 °С. Каждая кривая показывает, как неопределенность 1 мК в соответствующей ей реперной точке влияет на весь диапазон. Можно заметить, что в промежутке между реперными точками неопределенность иногда превышает неопределенность в самой точке. Суммарная кривая неопределенности при температурах в интервалах между точками может быть рассчитана с помощью суммирования кривых функций влияния.
Формула, для расчета неопределенности в интервале между реперными точками с использованием альтернативной записи функций МТШ-90 имеет следующий вид:
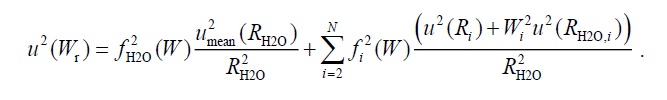
В этом методе предполагается отсутствие корреляции между измерениями в реперных точках. Данное допущение не приводит к большим неточностям, т.к. корреляция между точками может быть вызвана только применением одной электроизмерительной установки, все остальные компоненты, такие как параметры ампул и режимы печей различаются. Формула позволяет оценить неопределенность получаемого значения стандартной функции Wr, на основе измеряемого значения W при определенной температуре. Аргументами функции u2(Wr) являются стандартные неопределенности измерения сопротивления в реперных точках u(Ri) и неопределенности сопротивлений, измеренных после реперных точек в тройной точке воды u(RH2O i). Поскольку значение Wr связано со значением измеренной температуры (см. раздел «Расчет температуры по показаниям эталонного термометра»), неопределенность u(Wr) можно пересчитать в неопределенность измеренного значения температуры, используя производную стандартной функции dWr/dT.
u(T) = u(Wr)/(d Wr/dT).
Полное и подробное описание функций влияния для всех диапазонов МТШ-90, в которых используются платиновые термометры сопротивления, смотрите в монографии ККТ «Guide to the Realization of the ITS-90. Platinum Resistance Thermometry». В данной монографии также рассматриваются дополнительные источники неопределенности температуры, измеренной платиновым термометром сопротивления в диапазоне между реперными точками. Этими источниками являются три типа неединственности ( non-uniqueness) шкалы МТШ-90.

