Поверка ТС в термостате методом сличения с эталонным термометром сопротивления
Поверка ТС в термостате методом сличения с эталонным термометром сопротивления это наиболее распространенный способ поверки промышленных термометров сопротивления. Методика поверки и примеры расчета расширенной неопределенности поверки приводятся в ГОСТ 8.461-2009 (ГОСТ Р 8.624-2006), с которым можно ознакомиться в разделе Российские и межгосударственные стандарты Подробная методика поверки термометров сопротивления также приведена в разделе сайта "Поверка термометров сопротивления и чувствительных элементов". Расчет расширенной неопределенности поверки термометров сопротивления реализован в сертифицированной программе TCal-8-461.
Расчет неопределенности можно выполнить также "вручную", без программного обеспечения, основываясь на описанной ниже методике. Однако при этом необходимо обосновать все формулы и цифры при проведении аккредитации на право поверки и калибровки.
Учебные видео лекции о поверке промышленных термометров и расчете неопределенности публикуются по ссылкам:
1 лекция: https://youtu.be/wwRNaXpU47M
2 лекция: https://youtu.be/HUHNuYTzJNw
МЕТОДИКА РАСЧЕТА НЕОПРЕДЕЛЕННОСТИ ПОВЕРКИ ТС
При поверке в термостате происходит последовательное измерение температуры с помощью эталонного термометра и измерение сопротивления поверяемого ТС. Предлагается применить простейшие уравнения измерения:
Для эталонного термометра tx = ts,
где ts - среднее арифметическое значение из результатов измерения температуры, полученных по N измерениям.
Величина ts зависит от количества проведенных измерений, их разброса. На нее оказывает влияние точность измерительной аппаратуры, точность эталонного термометра и его нестабильность за межповерочный интервал, нестабильность температуры в термостате. В стандарте ЕА /4-02 для каждого источника неопределенности в уравнение измерений добавляется соответствующая поправка d t, как правило, равная нулю, но позволяющая идентифицировать все входящие величины, для включения их в бюджет неопределенностей. Для того, чтобы не вводить в заблуждение поверителей, мы не стали включать в уравнение нулевые члены.
Для поверяемого термометра Rx = Rs,
где Rs - среднее арифметическое значение из результатов измерения сопротивления, полученных по N измерениям.
Величина Rs зависит от количества проведенных измерений, их разброса. Основными влияющими факторами являются точность измерительной аппаратуры и градиент температуры в термостате.
Для того, чтобы привести стандартные неопределенности к одной размерности, их умножают на коэффициенты чувствительности: С1 – коэффициент чувствительности эталонного ТС dR/dt, Ом/°С, определяемый при температуре tS по уравнению, приведенному в свидетельстве о поверке ТС, С2 – коэффициент чувствительности поверяемого ТС dR/dt , Ом/°С, определяемый по уравнению НСХ ТС при температуре tx.
Бюджет неопределенности поверки ТС.
| Источник неопределенности | Исходные данные | Тип распределения | Метод расчета станд. неопределенности | Коэф. чувств. | |
| Бюджет неопределенности измерения температуры в термостате | |||||
| Случайные эффекты при измерении | Ri –результат изм. Nlab – кол-во изм. для предв. оценки N – кол-во изм. при поверке RS –среднее арифм. из Nlab изм. |
нормальное | 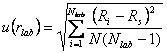 |
1/С1 | |
| Нестабильность температуры в термостате | ± δст - пределы колебаний темп. | равномерное |  |
1 | |
| Поверка эталонного термометра | UЭ – расширенная неопределенность поверки (из св-ва о поверке). См. примечание (2) | нормальное |  |
1 | |
| Электроизмерительная установка | ±Δпр - предел допустимой погрешности | нормальное | u(δrs )= Δпр/3 | 1/С1 | |
| ± ars - разрешающая способность установки | равномерное |  |
1/С1 | ||
| Нестабильность эталонного термометра за межповерочный интервал, равномер. распр. | ±aэ – возможное изменение в сопротивлении ТС за межповерочный интервал | равномерное |  |
1 | |
| Суммарная стандартная неопределенность температуры в термостате uc(tx), °С | 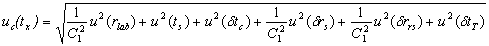 |
||||
| Бюджет неопределенности измерения сопротивления поверяемого термометра | |||||
| Случайные эффекты при измерении | Ri –результат i-го изм. Nlab – кол-во изм. для предв. оценки N – кол-во изм. при поверке RS –среднее арифм. из Nlab изм. |
нормальное | 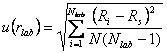 |
1 | |
| Электроизмерительная установка | ±Δпр - предел допустимой погрешности | нормальное | u(δrs )= Δпр/3 | 1 | |
| ± ars - разрешающая способность установки | равномерное |  |
1 | ||
| Перепад температуры в раб. объеме | ± aF – изменение температуры в рабочем объеме (на длине ЧЭ термометров) | равномерное | 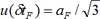 |
С2 | |
| Суммарная стандартная неопределенность измерения сопротивления uc(Rk), Ом | 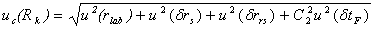 |
||||
Суммарная стандартная неопределенность uс(R) и расширенная неопределенность U поверки термометра в каждой температурной точке рассчитываются по формулам:
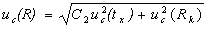
U = k . uc(R),
где k – коэффициент охвата, принимаемый равным 2 (вероятность нахождения результата в интервале ± U в предположении нормального закона распределения равна 95%).
Примечания:
1. Для того, чтобы оценить неопределенность, возникающую от случайных эффектов при измерении в конкретной лаборатории, необходимо предварительно оценить СКО единичного измерения при большом количестве измерений Nlab (более 50). Количество измерений, проводимых при поверке, N – как правило значительно меньше (1-5). Стандартная неопределенность рассчитывается как СКО среднего из N измерений.
2. Если в свидетельстве о поверке эталонного термометра не приведена расширенная неопределенность поверки, но приведен разряд термометра, то для расчета стандартной неопределенности доверительную погрешность, соответствующую данному разряду, следует разделить на 2.
3. В приведенном примере предполагается, что в сертификате на электроизмерительную установку дан предел допустимой погрешности (т.е. интервал, в котором при нормальном распределении попадает 99% результатов). Поэтому стандартная неопределенность u(δrs) (ско распределения) рассчитана как ± Δпр/3. Если в свидетельстве о поверке установки приводится расширенная неопределенность результата измерения U, то следует стандартную неопределенность определять как U/2.
4. Если установка (мост) работает с внешней образцовой мерой сопротивления и известны стандартная неопределенность uS измеряемого отношения S=RTC/Rобр, а также стандартная неопределенность градуировки меры
u(Rобр), то стандартную неопределенность измерения сопротивления u(δrs)определяют по формуле
u(δrs)= S2 u2(Rобр) + Rобр2 uS2.
5. При измерениях в сухоблочном термостате необходимо отдельно оценивать вертикальный и горизонтальный перепад температуры в рабочем объеме термостата. Если в результате исследований удалось определить постоянные поправки, то их следует ввести в результат, а их неопределенности – в бюджет неопределенностей.
Подробная методика поверки рабочих термометров сопротивления также приведена в разделе сайта "Поверка термометров сопротивления и чувствительных элементов"


